Volatility modelling: EWMA and GARCH#

  • Import the necessary packages

packages

acronyms

matplotlib.pyplot

plt

numpy

np

os

pandas

pd

scipy.optimize

spop

 
import matplotlib.pyplot as plt
import numpy as np
import os 
import pandas as pd 
import scipy.optimize as spop
import warnings

warnings.simplefilter('ignore')

  • Set your working directory using os.chdir([PATH]) (change directory).

#os.chdir(r'C:\Users\cdes1\OneDrive - ICHEC\Documents\Cours\PortfolioManagement')
os.chdir(r'/Users/christophe/OneDrive - ICHEC/Documents/Cours/PortfolioManagement')

  • Check that the working directory has been updated (os.getcwd()).

os.getcwd()

'/Users/christophe/Library/CloudStorage/OneDrive-ICHEC/Documents/Cours/PortfolioManagement'

S&P500#

  • Import the excel File sp500_daily.xlsx (in your data folder) as a DataFrame called df.

df = pd.read_excel('data/sp500_daily.xlsx', index_col=0, parse_dates=True)

  • Display the first 5 rows of this DataFrame (using df.head()).

df.head()
CLOSE
Date
1930-01-02 21.18
1930-01-03 21.23
1930-01-04 21.48
1930-01-06 21.50
1930-01-07 21.31

  • Display the last 5 rows of this DataFrame (using df.tail()).

df.tail()
CLOSE
Date
2022-12-23 3844.8150
2022-12-27 3829.2493
2022-12-28 3783.2219
2022-12-29 3849.2832
2022-12-30 3839.4966

  • Display some information about this DataFrame (using df.info()).

df.info()

<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 24060 entries, 1930-01-02 to 2022-12-30
Data columns (total 1 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   CLOSE   24060 non-null  float64
dtypes: float64(1)
memory usage: 375.9 KB

  • Rename the column “CLOSE” as “price”.

https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.rename.html

df.rename(columns={'CLOSE': 'price'}, inplace=True)
df
price
Date
1930-01-02 21.1800
1930-01-03 21.2300
1930-01-04 21.4800
1930-01-06 21.5000
1930-01-07 21.3100
... ...
2022-12-23 3844.8150
2022-12-27 3829.2493
2022-12-28 3783.2219
2022-12-29 3849.2832
2022-12-30 3839.4966

24060 rows × 1 columns

Line chart#

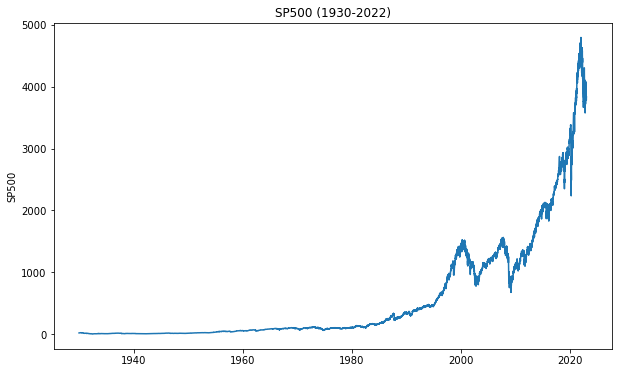
Create a line plot of the S&P500.

Set a label SP500 on the y-axis and a title (e.g., ’SP500 (1930-2022)’)

https://matplotlib.org/stable/gallery/index.html

https://stackoverflow.com/questions/34162443/why-do-many-examples-use-fig-ax-plt-subplots-in-matplotlib-pyplot-python

Save this figure in your folder images.

fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(df['price']) 
# ax.plot(df) also works because there is only one column in the DataFrame
plt.ylabel('SP500')
plt.title('SP500 (1930-2022)')
fig.savefig('images/volatility_sp500.png')
plt.show()
../../_images/ewma_20_0.png

  • Compute the logarithmic returns.

  • Remove the first missing row.

  • Rename the column “price” into “rets”

  • Display the first 5 rows.

rets = np.log(df / df.shift(1)).dropna() # rendement log 
rets.rename(columns={'price': 'rets'}, inplace=True)
rets.head()
rets
Date
1930-01-03 0.002358
1930-01-04 0.011707
1930-01-06 0.000931
1930-01-07 -0.008876
1930-01-08 -0.000939

  • Compute the volatility

“Classical formula”: Volatility is computed as the standard deviation of the returns. To annualize volatility, multiply by the square root of data frequency.

\[ \text{Volatility} = STD(R_t) \]
historical_volatility = np.std(rets) * np.sqrt(252)
historical_volatility

rets    0.182536
dtype: float64

Note: the [0] is needed in order to only get the number.

historical_volatility = np.std(rets) * np.sqrt(252)
historical_volatility

rets    0.182536
dtype: float64

We can also use [‘rets’].

historical_volatility = np.std(rets) * np.sqrt(252)
historical_volatility['rets']

0.1825362035297431

Alternatively, we can use the .std() method on the DataFrame.

rets.std() * np.sqrt(252) 

rets    0.18254
dtype: float64

Finally, a nice output, we can use format.

historical_volatility = np.std(rets) * np.sqrt(252)
historical_volatility = historical_volatility['rets']
print("{:.4%}".format(historical_volatility))

18.2536%

“Finance formula”: We can also make the simplifying assumption that \(\bar{r} = 0\). In this case, the variance is simply the sum of the squared returns.

\[ \sigma^2 = \frac{1}{m} \sum_{i=1}^m u^2_i \]
\[ \sigma = \sqrt{\sigma^2} \]
historical_volatility = np.sqrt(np.mean(rets**2, axis=0)) * np.sqrt(252) 
historical_volatility = historical_volatility[0]
print("{:.4%}".format(historical_volatility))

18.2568%

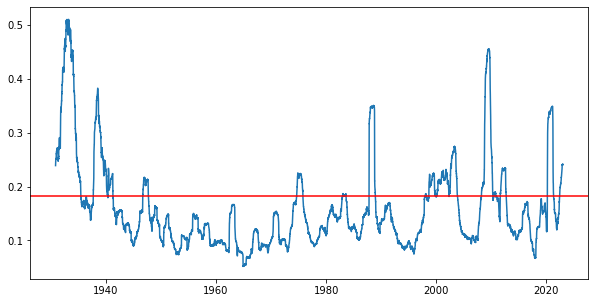
Rolling volatility

Volatility is not constant. Let’s compute it and plot it using a rolling window of 252 days (approximately 1 year).

rolling_vol = (rets.rolling(252).std()*np.sqrt(252))

fig, ax = plt.subplots(figsize=(10,5))
ax.plot(rolling_vol)
plt.axhline(historical_volatility, color='red')
plt.savefig('images/volatility_rolling_window_volatility.png')
plt.show();
../../_images/ewma_37_0.png

EWMA#

Using the returns from 2010, use the EWMA to model volatility

To make things visual, we will put everything inside the DataFrame, very similar to what we would have done in Excel.

rets = rets.loc['2010-01-01':].copy()
rets.head()
rets
Date
2010-01-04 0.015910
2010-01-05 0.003118
2010-01-06 0.000540
2010-01-07 0.004000
2010-01-08 0.002876

Compute the number of observations and store this value in n.

n = rets.shape[0]
n

3272

Compute the squared returns and store it in a new column rets_sq.

rets['rets_sq'] = rets['rets']**2
rets
rets rets_sq
Date
2010-01-04 0.015910 2.531178e-04
2010-01-05 0.003118 9.720487e-06
2010-01-06 0.000540 2.920861e-07
2010-01-07 0.004000 1.599607e-05
2010-01-08 0.002876 8.271171e-06
... ... ...
2022-12-23 0.005850 3.422799e-05
2022-12-27 -0.004057 1.645688e-05
2022-12-28 -0.012093 1.462353e-04
2022-12-29 0.017311 2.996689e-04
2022-12-30 -0.002546 6.480512e-06

3272 rows × 2 columns

Create a vector conditional of zero’s with size n and add this vector in a column conditional.

conditional = np.zeros(n)
rets['conditional'] = conditional
rets
rets rets_sq conditional
Date
2010-01-04 0.015910 2.531178e-04 0.0
2010-01-05 0.003118 9.720487e-06 0.0
2010-01-06 0.000540 2.920861e-07 0.0
2010-01-07 0.004000 1.599607e-05 0.0
2010-01-08 0.002876 8.271171e-06 0.0
... ... ... ...
2022-12-23 0.005850 3.422799e-05 0.0
2022-12-27 -0.004057 1.645688e-05 0.0
2022-12-28 -0.012093 1.462353e-04 0.0
2022-12-29 0.017311 2.996689e-04 0.0
2022-12-30 -0.002546 6.480512e-06 0.0

3272 rows × 3 columns

Initialize the second value as the squared value of the first return.

# rets.iloc[1]['conditional'] = rets.iloc[0]['rets']**2
# this results in a warning 
rets.loc[rets.index[1], 'conditional'] = rets.iloc[0]['rets_sq']
rets
rets rets_sq conditional
Date
2010-01-04 0.015910 2.531178e-04 0.000000
2010-01-05 0.003118 9.720487e-06 0.000253
2010-01-06 0.000540 2.920861e-07 0.000000
2010-01-07 0.004000 1.599607e-05 0.000000
2010-01-08 0.002876 8.271171e-06 0.000000
... ... ... ...
2022-12-23 0.005850 3.422799e-05 0.000000
2022-12-27 -0.004057 1.645688e-05 0.000000
2022-12-28 -0.012093 1.462353e-04 0.000000
2022-12-29 0.017311 2.996689e-04 0.000000
2022-12-30 -0.002546 6.480512e-06 0.000000

3272 rows × 3 columns

Initialize a variable lambda_val with a value of 0.94. Then, implement this formula:

\[ \sigma^2_n = \lambda \sigma^2_{n-1} + (1 - \lambda) u^2_{n-1} \]

Note 1: lambda cannot be used as variable name as it has another signification in Python.

Note 2: the vector rets has one additional observation in comparison to the vector conditional.

lambda_val = 0.94

for t in range(2, n):
    rets.loc[rets.index[t], 'conditional'] = lambda_val * rets.iloc[t-1]['conditional'] \
                                             + (1 - lambda_val) * rets.iloc[t-1]['rets'] ** 2
        
rets.head()
rets rets_sq conditional
Date
2010-01-04 0.015910 2.531178e-04 0.000000
2010-01-05 0.003118 9.720487e-06 0.000253
2010-01-06 0.000540 2.920861e-07 0.000239
2010-01-07 0.004000 1.599607e-05 0.000224
2010-01-08 0.002876 8.271171e-06 0.000212

Compute the loglikelihood as:

\[ \text{LogLikelihood}_i = - \ln(v_i) - \frac{u_i^2}{v_i} \]

where:

  • \(u_i\): return

  • \(v_i\): conditional

rets.loc[rets.index[1:], 'likelihood'] = -np.log(rets.iloc[1:]['conditional']) \
                                         -((rets.iloc[1:]['rets']**2)/rets.iloc[1:]['conditional'])
rets.head()
rets rets_sq conditional likelihood
Date
2010-01-04 0.015910 2.531178e-04 0.000000 NaN
2010-01-05 0.003118 9.720487e-06 0.000253 8.243253
2010-01-06 0.000540 2.920861e-07 0.000239 8.339858
2010-01-07 0.004000 1.599607e-05 0.000224 8.331539
2010-01-08 0.002876 8.271171e-06 0.000212 8.421147

Compute the sum of the log-likelihood into log_likelihood.

log_likelihood = rets['likelihood'].sum()
log_likelihood

27407.697995474882

Wrap everything within a function ewma_pandas, which takes two arguments: (1) the value of the lambda (lambda_val) and (2) the returns. This function returns the value of the loglikelihood.

def ewma_pandas(lambda_val, rets):
    df = rets.copy()
    n = df.shape[0]
    df['rets_sq'] = df['rets']**2
    conditional = np.zeros(n)
    df['conditional'] = conditional
    df.loc[df.index[1], 'conditional'] = df.iloc[0]['rets']**2
    for t in range(2, n):
        df.loc[df.index[t], 'conditional'] = lambda_val * df.iloc[t-1]['conditional'] \
                                             + (1 - lambda_val) * df.iloc[t-1]['rets'] ** 2
    df.loc[df.index[1:], 'likelihood'] = -np.log(df.iloc[1:]['conditional']) \
                                         -((df.iloc[1:]['rets']**2)/df.iloc[1:]['conditional'])
    log_likelihood = df['likelihood'].sum()
    return -log_likelihood

df = pd.read_excel('data/sp500_daily.xlsx', index_col=0, parse_dates=True)
rets = np.log(df/df.shift(1)).dropna()
rets.rename(columns={'CLOSE':'rets'}, inplace=True)
rets = rets.loc['2010-01-01':]
rets
rets
Date
2010-01-04 0.015910
2010-01-05 0.003118
2010-01-06 0.000540
2010-01-07 0.004000
2010-01-08 0.002876
... ...
2022-12-23 0.005850
2022-12-27 -0.004057
2022-12-28 -0.012093
2022-12-29 0.017311
2022-12-30 -0.002546

3272 rows × 1 columns

  • Call this function with a lambda value of 0.94. You should find the same value.

rets

ewma_pandas(0.94, rets)

-27407.697995474882

Naive optimization#

For different values of lambda between 0.80 and 1.00, compute the value of the different loglikelihood and plot it.

lambda_vals = np.arange(0.80, 1, 0.005)
log_vals = [-ewma_pandas(lam, rets) for lam in lambda_vals]
plt.plot(lambda_vals, log_vals);
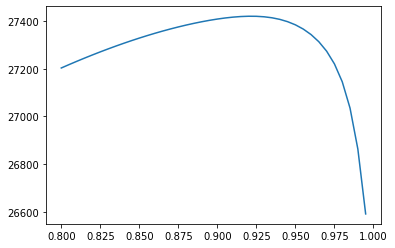
../../_images/ewma_60_0.png

We notice a maximum around 0.925. Let’s now optimize it to find the actual answer.

# reinitialize dataframe 
rets = np.log(df / df.shift(1)).dropna() # rendement log 
rets.rename(columns={'CLOSE': 'rets'}, inplace=True)
rets = rets.loc['2010-01-01':].copy()

var = np.std(rets)**2 # historical variance 
res = spop.minimize(ewma_pandas, var, rets, method="Nelder-Mead")
params = res.x
function = res.fun
print('Parameters: ', res.x)
print('LogLikelihood: ', -res.fun)

Parameters:  [0.92171991]
LogLikelihood:  27420.928807446242

lambda_val = res.x
df = rets.copy()
n = df.shape[0]
df['rets_sq'] = df['rets']**2
conditional = np.zeros(n)
df['conditional'] = conditional
df.loc[df.index[1], 'conditional'] = df.iloc[0]['rets']**2
for t in range(2, n):
    df.loc[df.index[t], 'conditional'] = lambda_val * df.iloc[t-1]['conditional'] \
                                         + (1 - lambda_val) * df.iloc[t-1]['rets'] ** 2

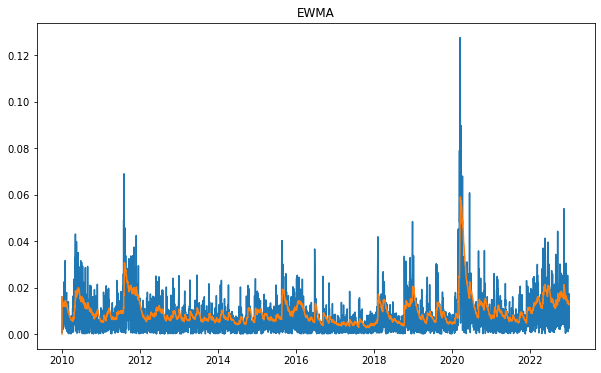
fig, ax = plt.subplots(figsize=(10,6))
ax.plot(np.abs(df['rets']))
ax.plot(df['conditional']**(1/2))
ax.set_title('EWMA')
plt.show()
../../_images/ewma_64_0.png 
%%time 

ewma_pandas(0.94, rets)

CPU times: user 447 ms, sys: 1.57 ms, total: 449 ms
Wall time: 448 ms

-27407.697995474882

Improve performance using numpy#

It is not easy nor efficient to fill a DataFrame. A better approach (although less beautiful) is to work with numpy arrays. Reimplement everything without using Pandas.

df = pd.read_excel('data/sp500_daily.xlsx', index_col=0, parse_dates=True)
rets = np.log(df / df.shift(1)).dropna() # rendement log 
rets.rename(columns={'CLOSE': 'rets'}, inplace=True)
rets = rets.loc['2010-01-01':]
rets = np.array(rets).ravel()
rets.shape
rets

array([ 0.01590968,  0.00311777,  0.00054045, ..., -0.01209278,
        0.01731095, -0.00254568])

n = len(rets)
n

3272

conditional = np.zeros(n-1)
conditional[0] = rets[0]**2
conditional

array([0.00025312, 0.        , 0.        , ..., 0.        , 0.        ,
       0.        ])

lambda_val = 0.94

for t in range(1, len(conditional)):
    conditional[t] = lambda_val * conditional[t-1] + (1 - lambda_val) * rets[t] ** 2
        
conditional

array([0.00025312, 0.00023851, 0.00022422, ..., 0.00017394, 0.00017228,
       0.00017992])

likelihood = -np.log(conditional)-((rets[1:]**2)/conditional)
likelihood

array([8.24325261, 8.33985817, 8.33153924, ..., 7.81607462, 6.92696348,
       8.58695739])

log_likelihood = np.sum(likelihood)
log_likelihood

27407.697995474882

It’s now time to wrap everything within a function ewma. We assume that we pass to the function two arguments:

  • the value of the lambda

  • a series of return in a ndarray

rets = np.array(rets)

def ewma_numpy(lambda_val, rets):
    n = len(rets)
    conditional = np.zeros(n-1)
    conditional[0] = rets[0]**2 
    for t in range(1, len(conditional)):
        conditional[t] = lambda_val * conditional[t-1] + (1 - lambda_val) * rets[t] ** 2
    likelihood = -np.log(conditional)-((rets[1:]**2)/conditional)
    log_likelihood = np.sum(likelihood)
    return -log_likelihood

Let’s check we get the same value of the logLikelihood using the function.

%%time 

ewma_numpy(lambda_val=0.94, rets=rets)

CPU times: user 2.42 ms, sys: 269 µs, total: 2.69 ms
Wall time: 2.49 ms

-27407.697995474882

It’s now time to optimize the function using spop.minimize.

var = np.std(rets)**2 # historical variance 
res = spop.minimize(ewma_numpy, [var], rets, method="Nelder-Mead")
params = res.x
function = res.fun
print('Parameters: ', res.x)
print('LogLikelihood: ', -res.fun)

Parameters:  [0.92171991]
LogLikelihood:  27420.928807446242

GARCH Modelling (NEDL)#

Now it’s your turn to implement the GARCH method.

df = pd.read_excel('data/sp500_daily.xlsx', index_col=0, parse_dates=True)
rets = np.log(df / df.shift(1)).dropna()
rets.rename(columns={'CLOSE': 'rets'}, inplace=True)
rets = rets.loc['2010-01-01':].copy()
rets = np.array(rets)
rets = rets.ravel()
mean = np.average(rets)
var = np.var(rets)

def garch_nedl(params):
    mu = params[0]
    omega = params[1]
    alpha = params[2]
    beta = params[3]
    long_run = (omega/(1-alpha-beta))**(1/2)
    resid = rets - mu
    realised = abs(resid)
    conditional = np.zeros(len(rets))
    conditional[0] = long_run
    for t in range(1, len(rets)):
        conditional[t] = (omega + alpha*resid[t-1]**2 + beta*conditional[t-1]**2)**(1/2)
    likelihood = 1/((2*np.pi)**(1/2)*conditional)*np.exp(-realised**2/(2*conditional**2))
    log_likelihood = np.sum(np.log(likelihood))
    return -log_likelihood

#bnds = tuple((0,1) for x in range(4))
res = spop.minimize(garch_nedl, [mean, var, 0, 0], 
                    #bounds=bnds, 
                    method='Nelder-Mead')
params = res.x
mu = params[0]
omega = params[1]
alpha = params[2]
beta = params[3]
long_run = (omega/(1-alpha-beta))**(1/2)
resid = rets - mu
realised = abs(resid)
conditional = np.zeros(len(rets))
conditional[0] = long_run
for t in range(1, len(rets)):
    conditional[t] = (omega + alpha*resid[t-1]**2 + beta*conditional[t-1]**2)**(1/2)
    
print('GARCH model parameters')
print('----------------------')
print('mu', str(round(mu, 6)))
print('omega', str(round(omega, 6)))
print('alpha', str(round(alpha, 6)))
print('beta', str(round(beta, 6)))

GARCH model parameters
----------------------
mu 0.000775
omega 4e-06
alpha 0.178418
beta 0.793665

fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(realised)
ax.plot(conditional)

[<matplotlib.lines.Line2D at 0x7fb3d8e45580>]
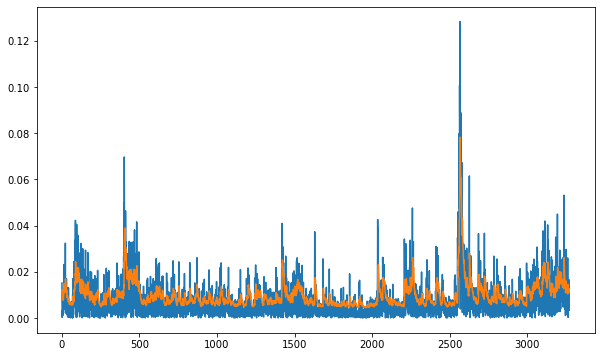
../../_images/ewma_85_1.png

Garch zero-mean#

def garch_zero_mean(params):
    # specifying model parameters
    mu = 0 
    omega = params[0]
    alpha = params[1]
    beta = params[2]
    # calculating long run volatility
    # long_run = (omega/(1 - alpha - beta))**(1/2)
    # calculating realized and conditional volatility
    resid = rets - mu
    realized = abs(resid)
    conditional = np.zeros(len(rets))
    conditional[0] = rets[0]**2
    for t in range(1, len(rets)):
        conditional[t] = (omega + alpha*resid[t-1]**2 + beta*conditional[t-1])
    # calculating loglikelihood
    likelihood = -np.log(conditional) - realized**2 / conditional
    log_likelihood = np.sum(likelihood)
    return -log_likelihood

#mean = np.average(returns)
var = np.std(rets)**2
bounds = [(0.0, 1.0)]*3

res = spop.minimize(garch_zero_mean, [var, 0, 0], bounds=bounds, method='Nelder-Mead')
mu = 0 
omega = res.x[0]
alpha = res.x[1]
beta = res.x[2]
log_likelihood = -float(res.fun)
# calculating realized and conditional volatility
# long_run = (omega/(1 - alpha - beta))**(1/2)
resid = rets - mu
realized = abs(resid)
conditional = np.zeros(len(rets))
conditional[0] = rets[0]**2
for t in range(1, len(rets)):
    conditional[t] = (omega + alpha*resid[t-1]**2 + beta*conditional[t-1]**2)**(1/2)

likelihood = -np.log(conditional) - realized**2 / conditional
log_likelihood = np.sum(likelihood)

print('GARCH model parameters')
print('----------------------')
print('mu', str(round(mu, 6)))
print('omega', str(round(omega, 6)))
print('alpha', str(round(alpha, 6)))
print('beta', str(round(beta, 6)))
# print('long-run volatility', str(round(long_run, 4)))
print('log-likelihood', str(round(log_likelihood, 4))) 

GARCH model parameters
----------------------
mu 0
omega 7.7e-05
alpha 0.385073
beta 0.0
log-likelihood 14968.3621

fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(realised)
ax.plot(conditional)

[<matplotlib.lines.Line2D at 0x7fb3d8cddf70>]
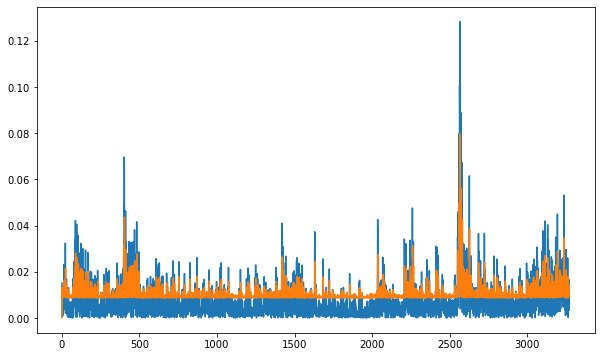
../../_images/ewma_90_1.png

ARCH package#

https://arch.readthedocs.io/en/latest/index.html

# !pip install arch
from arch import arch_model

am = arch_model(rets*100)
res = am.fit()
print(res.summary())

Iteration:      1,   Func. Count:      6,   Neg. LLF: 45190.138944107726
Iteration:      2,   Func. Count:     17,   Neg. LLF: 19000.159297830152
Iteration:      3,   Func. Count:     27,   Neg. LLF: 6719.894415448125
Iteration:      4,   Func. Count:     34,   Neg. LLF: 8186.897239907136
Iteration:      5,   Func. Count:     40,   Neg. LLF: 4525.832689694671
Iteration:      6,   Func. Count:     47,   Neg. LLF: 4243.099399974918
Iteration:      7,   Func. Count:     53,   Neg. LLF: 4241.2416896886125
Iteration:      8,   Func. Count:     58,   Neg. LLF: 4241.24076531225
Iteration:      9,   Func. Count:     63,   Neg. LLF: 4241.240763542724
Iteration:     10,   Func. Count:     67,   Neg. LLF: 4241.240763542601
Optimization terminated successfully    (Exit mode 0)
            Current function value: 4241.240763542724
            Iterations: 10
            Function evaluations: 67
            Gradient evaluations: 10
                     Constant Mean - GARCH Model Results                      
==============================================================================
Dep. Variable:                      y   R-squared:                       0.000
Mean Model:             Constant Mean   Adj. R-squared:                  0.000
Vol Model:                      GARCH   Log-Likelihood:               -4241.24
Distribution:                  Normal   AIC:                           8490.48
Method:            Maximum Likelihood   BIC:                           8514.85
                                        No. Observations:                 3272
Date:                Thu, Apr 06 2023   Df Residuals:                     3271
Time:                        16:11:37   Df Model:                            1
                                Mean Model                                
==========================================================================
                 coef    std err          t      P>|t|    95.0% Conf. Int.
--------------------------------------------------------------------------
mu             0.0776  1.326e-02      5.857  4.708e-09 [5.166e-02,  0.104]
                              Volatility Model                              
============================================================================
                 coef    std err          t      P>|t|      95.0% Conf. Int.
----------------------------------------------------------------------------
omega          0.0369  7.769e-03      4.744  2.100e-06 [2.163e-02,5.208e-02]
alpha[1]       0.1801  2.365e-02      7.616  2.609e-14     [  0.134,  0.226]
beta[1]        0.7932  2.206e-02     35.960 3.542e-283     [  0.750,  0.836]
============================================================================

Covariance estimator: robust

fig = res.plot(annualize="D")
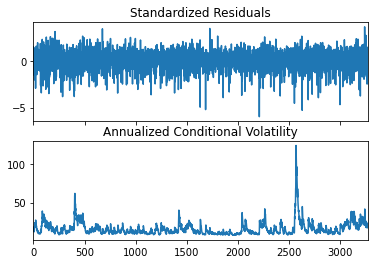
../../_images/ewma_94_0.png

References and further ressources#

NEDL - ARCH model - volatility persistence in time series (Excel)

https://www.youtube.com/watch?v=-G5g3ChktEs

NEDL - GARCH model - volatility persistence in time series (Excel)

https://www.youtube.com/watch?v=88oOzPFVWTU

NEDL - GARCH model in Python

https://www.youtube.com/watch?v=3boMYvIzGQ8