Fonctions#

Définition

La programmation est l’art d’apprendre à un ordinateur comment accomplir des tâches qu’il n’était pas capable de réaliser auparavant. L’une des méthodes les plus intéressantes pour y arriver consiste à ajouter de nouvelles instructions au langage de programmation que vous utilisez sous la forme de fonctions originales (Swinnen, 2012).

La synthaxe pour définir une fonction est la suivante:

Utiliser le mot clé def
Donner un nom à la fonction
Indiquer les arguments entre parenthèses
: et passer à la ligne
Instructions de la fonction
Finir par le mot clé return et ce qui est renvoyé par la fonction

La fonction \(f(x) = x^2\) permet de calculer le carré d’un nombre. Nous appellons cette fonction carre_aire. Cette fonction n’a besoin que d’un seul argument, cote, qui est la seule information nécessaire. En effet, si nous connaissons la longueur du côté du carré, nous pouvons calculer l’aire.

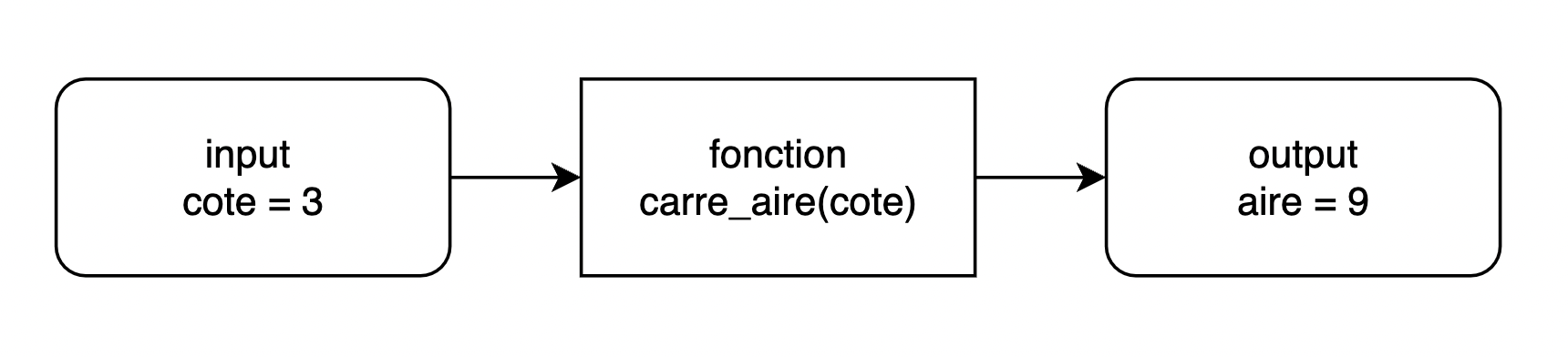
def carre_aire(cote):
    aire = cote**2
    return aire

Quand la fonction carre_aire reçoit le chiffre 3, elle exécutera certaines instructions de telle sorte à renvoyer la valeur 9. Cette valeur sera stockée dans la variable aire. Il n’est pas nécessaire que le nom de la variable à côté du return soit identique au nom de la variable dans lequel on stocke le résultat de la fonction.

aire = carre_aire(cote=3)
print(aire)

Remarque: on peut ne pas indiquer le nom du paramètre dans la parenthèse.

aire = carre_aire(3)
print(aire)

Lorsque le nombre d’instructions est relativement peu élevé, comme c’est le cas ici, nous pouvons directement renvoyer la valeur sans la stocker temporairement dans une variable.

def carre_aire(cote):
    return cote**2

On peut tester à nouveau la fonction en passant la valeur 5. On peut également afficher directement le résultat renvoyé par la fonction, sans stocker ce résultat dans une variable.

print(carre_aire(5))

Fonctions à plusieurs arguments#

La fonction carre_aire ne possède qu’un seul argument (un seul input). Nous allons créer une fonction qui calcule l’aire d’un rectangle, rectangle_aire qui a besoin de 2 arguments, la longueur et la largeur du rectangle. Nous calculerons ensuite l’aire d’un rectangle dont la longueur est 5cm et la largeur est 3cm.

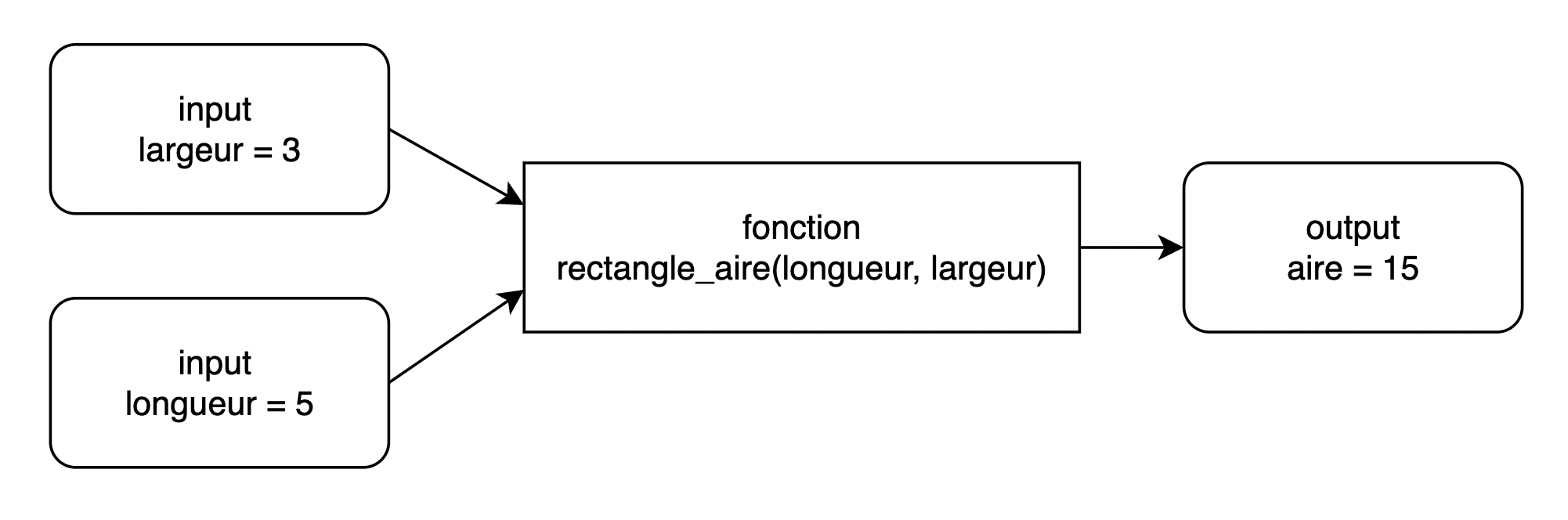
def rectangle_aire(longueur, largeur):
    aire = longueur * largeur
    return aire

longueur=5
largeur=3
aire = rectangle_aire(longueur, largeur)
print(aire)

Pourquoi utiliser des fonctions ?#

L’avantage d’utiliser une fonction est de pouvoir réutiliser des morceaux de code. Supposons que nous avons deux listes dont nous devons calculer la moyenne. Nous pouvons calculer les deux moyennes de la façon suivante (les différents éléments de syntaxe seront abordés plus tard dans le cours):

a = [2, 5, 3, 8, 6]
b = [5, 2, 1, 7, 4]

# calculer la moyenne de la liste a 
somme_a = 0
for i in range(len(a)):
    somme_a = somme_a + a[i]
moyenne_a = somme_a / len(a)
print(moyenne_a)

# calculer la moyenne de la liste b
somme_b = 0
for i in range(len(b)):
    somme_b = somme_b + b[i]
moyenne_b = somme_b / len(b)
print(moyenne_b)

4.8
3.8

Nous remarquons cependant que le code nécessaire pour calculer la moyenne est évidemment similaire et il n’est pas utile ni efficient de procéder de la sorte. Le code suivant permet de calculer la moyenne de 2 listes à l’aide d’une fonction.

a = [2, 5, 3, 8, 6]
b = [5, 2, 1, 7, 4]

def moyenne(liste):
    somme = 0
    for i in range(len(liste)):
        somme = somme + liste[i]
    moyenne = somme / len(liste)
    return moyenne

moyenne_a = moyenne(a)
moyenne_b = moyenne(b)
print(moyenne_a)
print(moyenne_b)

4.8
3.8

Arguments par défaut#

Nous allons créer une fonction tvac qui permet de calculer un montant TVAC sur base d’un montant HTVA (htva) et d’un taux de tva (taux_de_tva).

Testons ensuite cette fonction si htva = 1000 et taux_de_tva = 0.21. Nous faisons appel à la fonction et stockons le résultat dans montant_tvac. Finalement, nous affichons cette variable.

Pour rappel:

\[ TVAC = HTVA \times (1 + \text{taux de tva}) \]

def tvac(htva, taux_de_tva):
    tvac = htva * (1+taux_de_tva)
    return tvac

montant_tvac = tvac(htva=1000, taux_de_tva=0.21)
print("TVAC:", montant_tvac)

TVAC: 1210.0

Nous savons que le taux normal de TVA en Belgique est de 21%. Nous pouvons considérer que c’est une valeur par défault pour l’argument taux_de_tva. Dans ce cas, nous indiquons cette valeur lors de la définition de la fonction.

def tvac(htva, taux_de_tva=0.21):
    tvac = htva * (1+taux_de_tva)
    return tvac

Ensuite, il y a plusieurs possibilités lors de l’appel de la fonction:

J’indique que le taux de tva est de 21%

montant_tvac = tvac(htva=1000, taux_de_tva=0.21)
print("TVAC:", montant_tvac)

TVAC: 1210.0

Je n’indique rien et la fonction utilise l’argument par défault

montant_tvac = tvac(htva=1000)
print("TVAC:", montant_tvac)

TVAC: 1210.0

J’indique un autre chiffre que l’argument par défault

montant_tvac = tvac(htva=1000, taux_de_tva=0.06)
print("TVAC:", montant_tvac)

TVAC: 1060.0

Lorsque les paramètres sont indiqués, il n’est pas nécessaire de passer les arguments dans l’ordre.

montant_tvac = tvac(taux_de_tva=0.06, htva=1000)
print("TVAC:", montant_tvac)

TVAC: 1060.0

Exercice - partie 1#

Créer une fonction polynome qui calcule et affiche les racines d’un polynôme de degré 2. Calculez les racines du polynôme

\[x^2 + 3x - 4\]

Dans un premier temps, il faut calculer \(\Delta\):

\[ \Delta = b^2 - 4ac \]

Ensuite les deux racines, \(r_1\) et \(r_2\) sont:

\[ r_1, r_2 = \frac{-b \pm \sqrt{\Delta}}{2a} \]

Stocker les valeurs des racines dans rac1 et rac2, et affichez leurs valeurs respectives.

def polynome(a, b, c):
    delta = b**2 - 4*a*c
    rac1 = (-b + delta**0.5)/(2*a)
    rac2 = (-b - delta**0.5)/(2*a)
    print(rac1)
    print(rac2)
    
polynome(1, 3, -4)

1.0
-4.0

Modifier la fonction de telle sorte à ce qu’elle renvoie les valeurs (sans les afficher au sein de la fonction).

def polynome(a, b, c):
    delta = b**2 - 4*a*c
    rac1 = (-b + delta**0.5)/(2*a)
    rac2 = (-b - delta**0.5)/(2*a)
    return rac1, rac2 

r1, r2 = polynome(1, 3, -4)
print("Racine 1:", r1)
print("Racine 2:", r2)

Racine 1: 1.0
Racine 2: -4.0

Avant de poursuivre plus loin dans la création de fonctions, nous avons besoin de découvrir d’autres notions:

Les listes
Les instructions répétitives (boucle for)
Les instructions conditionnelles (if et while)

Ces différents points de matière sont abordés dans les prochains chapitres.

Les fonctions - partie 2#

Retour d’une fonction#

Jusqu’à présent, chaque fonction retourne une valeur. C’est le plus souvent le cas. Il est toutefois possible de créer une fonction qui ne retourne rien. Par exemple, une fonction qui ne s’occupe que de l’affichage d’une matrice.

def print_matrix(mat):
    for i in range(len(mat)):
        for j in range(len(mat[i])):
            print(mat[i][j], end="\t")
        print("")

m = [[1,2,3],[4,5,6]]

print_matrix(m)

1	2	3	
4	5	6	

Dans ce cas, la fonction ne possède pas de return. Elle renverra donc None si jamais on affecte le retour de la fonction à une variable (par erreur).

def print_matrix(mat):
    for i in range(len(mat)):
        for j in range(len(mat[i])):
            print(mat[i][j], end="\t")
        print("")

m = [[1,2,3],[4,5,6]]

display_matrix = print_matrix(m)
print(display_matrix)

1	2	3	
4	5	6	
None

Imbriquer des fonctions#

Une fonction peut faire appel à une autre fonction. Reprenons l’exemple du calcul des racines d’un polynôme. Nous pourrions créer dans un premier temps une fonction qui calcule le \(\Delta\). Ensuite, la fonction polynome ferait appel à cette fonction delta.

def delta(a, b, c):
    return b**2 - 4*a*c

def polynome(a, b, c):
    d = delta(a, b, c)
    r1 = (-b + d**0.5)/(2*a)
    r2 = (-b - d**0.5)/(2*a)
    print(r1)
    print(r2)
    
polynome(a=1, b=3, c=-4)

1.0
-4.0

La portée des variables#

Quand une variable est définie au sein d’une fonction, elle n’existe qu’au sein de cette fonction. Il n’est donc pas possible d’y faire référence en dehors de cette fonction.

def add_1(x):
    x = x + 1
    return x

a = 3
print(a)
a = add_1(a)
print(a)
print(x)

3
4

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Input In [12], in <cell line: 9>()
      7 a = add_1(a)
      8 print(a)
----> 9 print(x)

NameError: name 'x' is not defined

Il y a une exception à cette règle. Si le mot-clé global est utilisé, ceci permet d’accéder à cette variable, sans qu’elle soit initialisée au sein de la fonction, ni passée comme argument.

def add_1():
    global a
    a = a + 1
    return a

a = 3
print(a)
add_1()
print(a)

3
4

Il est également possible d’accéder à la valeur d’une variable qui se trouve en dehors de la fonction.

x = 2 

def add_x(a):
    a = a + x
    return a
    
y = 5
y = add_x(y)
print(y)

Fonctions récursives#

Une fonction récursive est une fonction qui fait appel à elle-même.

Un exemple connu de fonction récursive est la fonction factorielle.

La factorielle d’un nombre est obtenue de la façon suivante:

\[ x! = x \times (x-1)! \]

\[ 0! = 1! = 1 \]

Voici un tableau pour la factorielle des chiffres de 0 à 5:

x	x !
0	1
1	1
2	2
3	6
4	24
5	120

def factorial(a):
    if a <= 1:
        return 1
    else:
        return a * factorial(a-1)

Nous appelons la fonction au sein d’une boucle de manière à afficher le contenu du tableau précédent.

for i in range(6):
    print(i, factorial(i))

Remarque 1: Dans la définition de la fonction, nous voyons en effet que la fonction factorial fait appel à elle-même. Ceci ne fonctionnera que si nous indiquons également un cas de base, dans ce cas, le cas de base est de renvoyer 1 si x <= 1.

Remarque 2: Une fonction récursive peut également être codée de manière non-récursive.

def factorial(x):
    f = 1 
    for i in range(1, x+1):
        f = f * i 
    return f

for i in range(6):
    print(i, factorial(i))

Exercices - partie 2#

Exercice 1#

Réaliser une fonction qui permet d’afficher les tables de multiplication et qui prend 2 arguments (a, le nombre à multiplier et b, le nombre de fois qu’il faut le multiplier). Cette fonction ne renvoie rien.

def table_de_multiplication(a, b):
    for i in range(1, b+1):
        print(a, "*", i, "=", a*i)

a = 8
b = 5
table_de_multiplication(a, b)

* 1 = 8
* 2 = 16
* 3 = 24
* 4 = 32
* 5 = 40

Exercice 2#

Supposez que vous avez 5 boules numérotées de 1 à 5 dans un sac et que vous devez en tirer 2 sans remise. Quel est le nombre de possibilités différentes? Si vous connaissez votre cours de probabilité, vous savez que vous devez utiliser la combinaison où \(n\) représente le nombre total de boules et \(p\) le nombre de boules tirées.

La combinaison se calcule via la formule suivante:

\[ _pC_n = \frac{n!}{p!(n-p)!} \]

Dans l’exemple:

\[ _2C_5 = \frac{5!}{2!(5-2)!} = \frac{120}{2 \times 6} = 10 \]

Pour vérifier, on notera que les 10 choix sont:

1-2 / 1-3 / 1-4 / 1-5

2-3 / 2-4 / 2-5

3-4 / 3-5

4-5

def combinaison(n, p):
    c = factorial(n) / (factorial(p)*factorial(n-p))
    c = int(c)
    return c 

print(combinaison(5, 2))

Exercice 3#

Et si l’ordre dans lequel les boules sont tirées a de l’importance ?

Alors, on parle d’un arrangement et la formule est la suivante:

\[ _pA_n = \frac{n!}{(n-p)!} \]

Dans l’exemple:

\[ _2A_5 = \frac{5!}{(5-2)!} = \frac{120}{6} = 20 \]

C’est logique! On a deux fois plus de possibilités que dans l’exemple précédent. Tirer d’abord la boule n°1 et ensuite la n°2 et inversément compte pour 2 possibilités différentes!

def arrangement(n, p):
    a = factorial(n) / factorial(n-p)
    a = int(a)
    return a

print(arrangement(5, 2))

Exercice 4#

Le triangle de Pascal est un tableau qui calcule la combinaison entre \(n\), le numéro de la ligne, et \(p\), le numéro de la colonne. Bien sûr, \( n \geq p\).

Si on génère ce tableau, on constate que chaque chiffre correspond à la somme de son voisin supérieur et de son voisin supérieur gauche.

def combinaison_table():
    print("", end="\t")
    for i in range(1, 11):
        print(i, end="\t")
    print("\n")
    for i in range(1,11):
        print(i, end="\t")
        for j in range(1,i+1):
            print(int(combinaison(i,j)), end="\t")
        print("\n")
        
combinaison_table()

2	3	4	5	6	7	8	9	10	

1	

2	1	

3	3	1	

4	6	4	1	

5	10	10	5	1	

6	15	20	15	6	1	

7	21	35	35	21	7	1	

8	28	56	70	56	28	8	1	

9	36	84	126	126	84	36	9	1	

10	45	120	210	252	210	120	45	10	1

Homepage

Fonctions

Contents